√100以上 特別 な 直角 三角形 350311

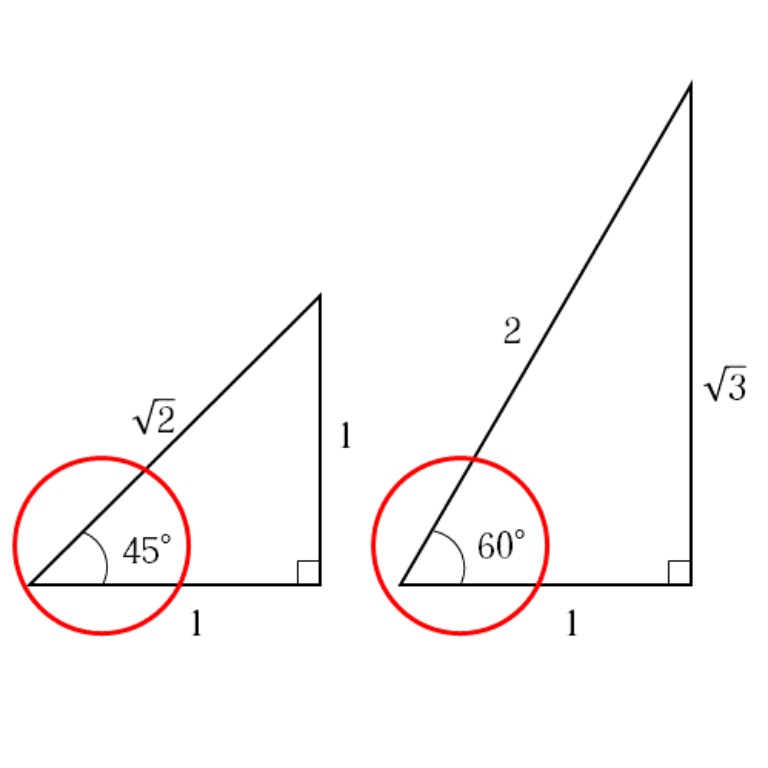
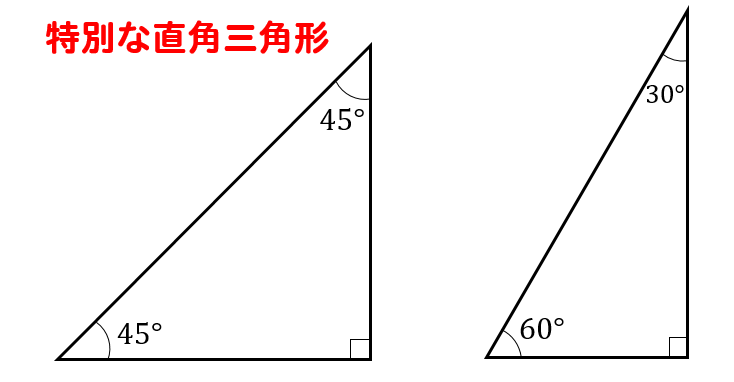
三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \2\ 種類あります。 その \2\ 種類は必ず暗記すべき特別な直角三角形です。 45 45 90 まずはじめに直角二等辺三角形タイプです。解説 ①→②→③の順に求める。 1つの角が60°の直角三角形だから 4√3①=√31 → ①=4 → ②=2 → ③ 2 = (4√3) 2 2 2 ③=2√13 問題1 (所要時間の目安：各々1分程度) (1) 次の二等辺三角形ABCの高さAHを求めなさい。 AH＝ BH=6を用いて直角三角形ABHに三平方の定理を適用します。 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な直角三角形の三つの内角の角度も簡単な数字で表される。 目次 非表示 1三角形の内角の和 2直角三角形とは 3直角三角形の辺の名称 4比とは 「a：b=2：1」の式に込められている情報 「a：b=4：2」の式に込められて

二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

特別 な 直角 三角形

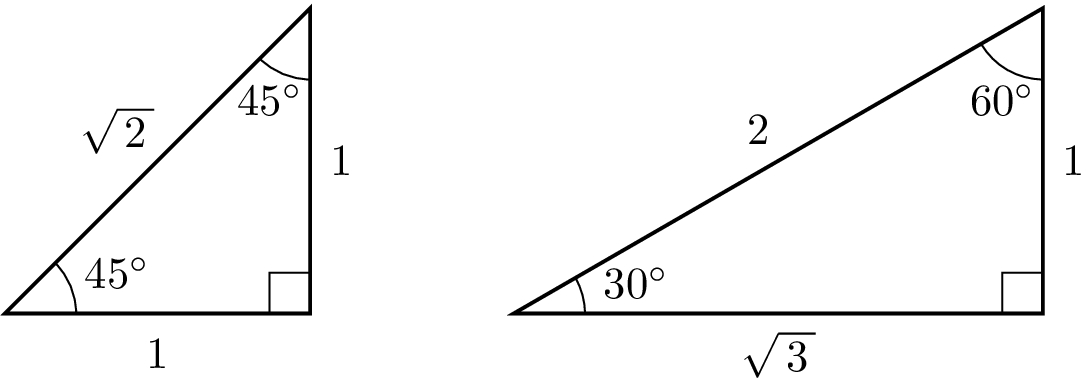
特別 な 直角 三角形- 特別な直角三角形の辺の比 三平方の定理では、特別な 直角三角形辺の比 を使って、三角形の辺の長さなどを求めることが出来ます。 基本事項をしっかり覚えて、素早く計算出来るように練習することが大切になります。や が出てくるのは，次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため，3つの角が30°，60°，90°である直角三角形と，45°，45°，90°である直角三角形の3辺の長さには，それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°，60°，90°の 直角三角形 45°，45°，90°の 直角三角形 3辺の比は となり

三平方の定理の利用 １ きっずゼミ子育て応援ブログ

 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角形タイプです。直角三角形である。 (2) 9cm, 8cm, 4cm 9が最も長いのでc 2 = 81 a 2 b 2 = 64 16 =80 よってa 2 b 2 ≠ c 2 となるので 直角三角形ではない。 確認 次の長さを3辺とする三角形のうち、直角三角形をすべて選べ。 答表示  数学直角三角形で形作り 中学部1段階想定。 画面の空白を押すだけで黒い直角三角形の色板を表示できるプレゼン教材です。 直角三角形を組み合わせて表示させることで，正方形や長方形，ひし形，風車，魚などなど，いろいろな形を作ることができます。 活用し 続きを読む 数学直角三角形で形作り Teach U特別支援教育のためのプレゼン教材

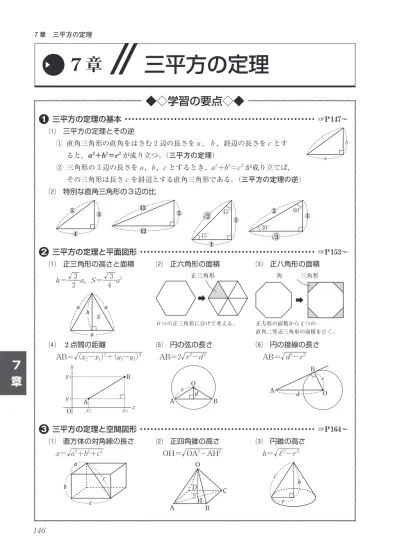
中3数学三平方の定理特別な直角三角形です。 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features2 特別な三角形 ここでは，よく使われる特別な直角三角形の辺の比について学習してみましょう。 特別な直角三角形 ① 直角二等辺三角形 ② 30 °，60 °，90 °の直角三角形 11 2：： 132：： ③ 整数比の辺をもつ直角三角形 345：： ：：特別な直角三角 形の辺の比を利 用し、いろいろ な図形の線分の 長さを求めるこ とができる。 正方形の対角線の長さを求 めること 正三角形の高さを求めるこ と 長方形の対角線や二等辺三 角形の高さを求めること 特別な直角三角形の辺の長 さの比

从已知两边求角度 若我们知道 直角三角形 两条边的长度，我们便可以求三角形的未知角度。 例子 梯子搁在墙上，如图。 梯子与墙之间的 角度 是多少？ 特別な直角三角形を使った練習問題です。 ➊特別な直角三角形については、「 1：2：√3 」と「 1：1：√2 」が有名ですが、その他「 1：2：√5 」「 3：4：5 」「 5：12：13 」も合わせて覚えておくと便利です。特殊な三角形のペア 18 年9 月19 日の朝日新聞朝刊に「世界に1 つだけの『三角 形ペア』発見 慶大院生2 人証明」との記事が載った． 世界に1 組だけ，特別な関係を把つ三角形が存在する―．図形を

高校入試 英語 数学 特別な直角三角形

Tossランド 特殊な直角三角形の三角比 の指導

次の直角三角形の長さの比を に書き入れなさい。 ③ ④ 正三角形 cm y cm ／6点 1 45° 4 30° 45° 60° 45° x 7 NO 1 60° 2 4 x 60° 10 y 45° x x 三平方の定理 2 特別な三角形112つの三角定規！ 今回は、 「特別な2つの直角三角形」 について学習するよ。 ここまでいろいろな直角三角形を見てきたけれど、その中に2つだけ。 絶対に暗記しておきたい直角三角形があるんだ。 それは、 「30°、60°、90°」 の直角三角形と、 「45°、45S：「そういえば直角三角形だ．」 s：「先生，他の特別な合同条件ってあるんですか？」 角三角形の合同条件」がありそうである t：「特別な合同条件ですね．では今日は，特殊な三 角形である「直角三角形」に焦点を当て，合同

三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori

パソコン講師の雑記録 直角三角形

3・三角形，四角形 技三角形や四角形を を分別すること 分別したり，格子 ができる。 点を結んで作図し たりすることがで きる。 2 長方形と正方形 4・身の回りからか 技紙を折って，直角 どに形が直角な を作ることができ ものを見つけ， る。 「直角」の ご活用ください。 白い直角三角形を押すと黒になり，もう一度押すと白に戻ります。 押す度に黒→白→黒と入れ替わり続けます。 似た動きをするTU Parts 他の直角三角形のTU Parts Fol 続きを読む A072 TUP押すと色が変わる直角三角形 (2色) Teach U特別支援教育のためのプレゼン教材サイト 2 コメントする活動を通して正方形，長方形，直角三角形への理解が求められている。 5 児童の実態 本学級の児童は，前学年で，様々な形を構成したり分解したりする活動を通して，図形を 理解したりその性質を見出したりするための基礎を経験してきている。

特別な直角三角形の３辺の比 の問題が分からないんですけど やり方を教えてください Clear

高校入試と いろいろな三角形の定義と定理について 中学生 受験対応 英語 数学 学習講座

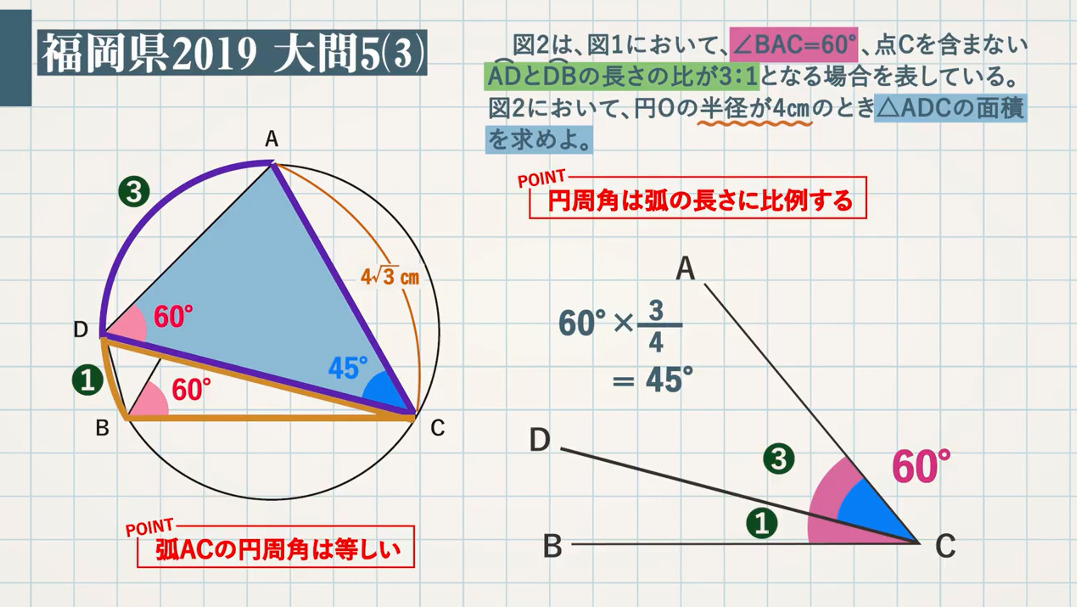
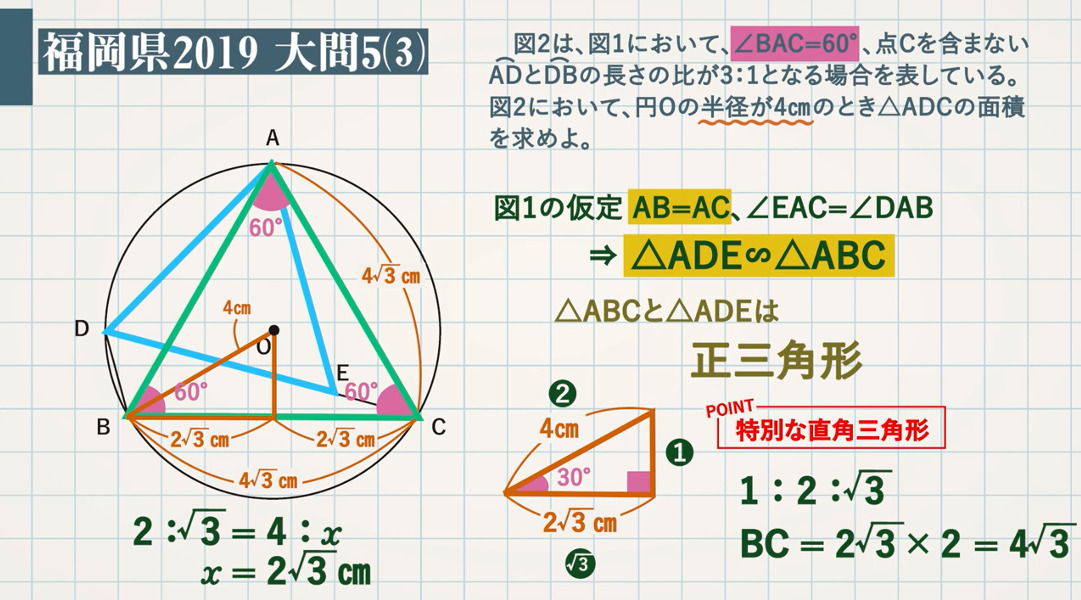
・正方形の対角線の長さの求め方 ・正三角形の高さの求め方 ・45°、60°をもつ直角三角形 小学生・中学生が勉強するならスクールtv。全国の学校の教科書に対応した動画で学習できます。授業の予習・復習にぴったり。直角のある三角形が直角三角形であるこ とを知る。 ・いろいろな形の中から直角三角形を見つ けることができる。 ☆直角三角形の定義を知り，その意 味を理解している。（考） ☆いくつかの形の中から，直角三角 形を見つけることができる。(技) 11POINT：特別な直角三角形（ $\textcolor{blue}{12\sqrt{3}} $) $\rm BO$ (斜辺) $=\rm 4cm$ の特別な直角三角形なので、$2\sqrt{3}=4\rm \frac{1}{2}BC$ これを解いて、$\textcolor{blue}{\rm BC=4\sqrt{3} cm }$ 。 ABCは正三角形なので、$\textcolor{blue}{\rm AC=4\sqrt{3} cm}$ となります。

直角三角形の新着記事 アメーバブログ アメブロ

動画コンテンツ一覧 算数 数学 英語塾のフェルマータ

 熊本大学教育学部附属特別支援学校 教諭 熊本大学大学院教育学研究科教職実践開発専攻 特別支援教育実践高度化コース 非常勤講師(年度～) ★「Teach U」管理者 ★モリサワUDフォント・エバンジェリスト ★(公財)学習情報研究センター三角定規には、\(\boldsymbol{45^{\circ}}\) の角を持つ直角二等辺三角形と、\(\boldsymbol{30^{\circ},\;60^{\circ}}\) の角を持つ直角三角形の \(2\) 種類があり、それぞれ 特別な \(\boldsymbol{3}\) 辺の長さの比 を持ちます。ADCは直角二等辺三角形になるので、 AD=DCで、ADAC=1 2 である。 よって AD6=1 2 AD=DC=3 2 ABDは60°、30°、90°の直角三角形なので ADBD=1 3 よって3 2BD=1 3 BD=3 6 すると高さが3 2 で、 底辺が3 6 3 2 である。 よって面積は 3 2 ×(3 6 3 2)÷2 =9 3 9 6cm 6cm 30° 60° 45° 45° 3√2cm 3√2cm 3√6cm A B C D

メルカリ 数学要点プリント 参考書 0 中古や未使用のフリマ

円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者

 A072 TUP押すと色が変わる直角三角形 (2色) 「TU Parts」です。 ご活用ください。 白い直角三角形を押すと黒になり，もう一度押すと白に戻ります。 押す度に黒→白→黒と入れ替 画面の空白を押すだけで黒い直角三角形の色板を表示できるプレゼン教材です。 直角三角形を組み合わせて表示させることで，正方形や長方形，ひし形，風車，魚などなど，いろいろな形を作ることができます。 数学直角三角形で形作り ， 数学直角三角形で形作り (枠あり) の枠をON/OFFできるバージョンです。 画面左下の 囲みの「＃」を押すと枠が特別な直角三角形を使えそうな角度がわかっている場合、垂線を引くなどして特別な直角三角形を作る。 角度は30°60°45°のほか1°や75°,105°などに注目して特別な直角三角形を作る。 xの値を求めよ。 A B C 7 8 x 1° ∠ACB=1°に着目し、その外角の60°を使って特別な直角三角形を作る。 A B C 7 8 x 1° D 60° 4 4 3 11 頂点AからBCの延長線上に垂線をおろし交点をDとする

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

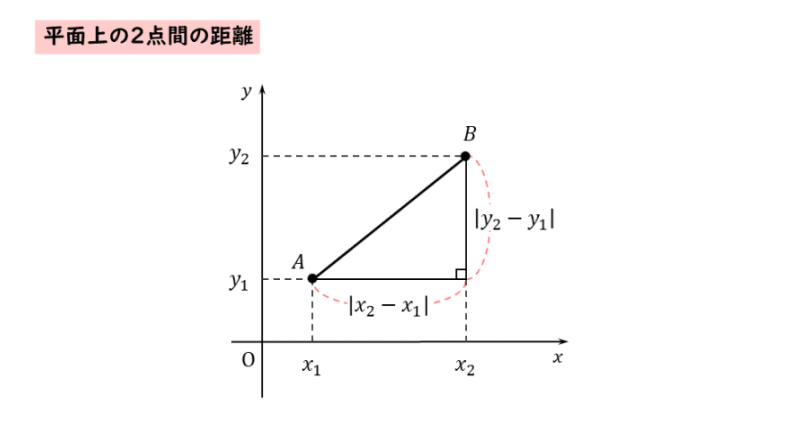
図形と方程式 ２点間の距離と三角形の形状について 日々是鍛錬 ひびこれたんれん

6 改めてサンキュー 直角三角形 オトナのための中学数学 天狼院書店

高校入試 英語 数学 三平方の定理

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

三 平方 の 定理 計算 C言語入門 Documents Openideo Com

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

はしご直角三角形

中3数学 三平方の定理 空間図形への利用 練習問題

Www2 Osaka C Ed Jp Blog Momodani C Blog Name 5d6cfa30ef2ad2771fbe8d80 Pdf

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

Am3hy

3

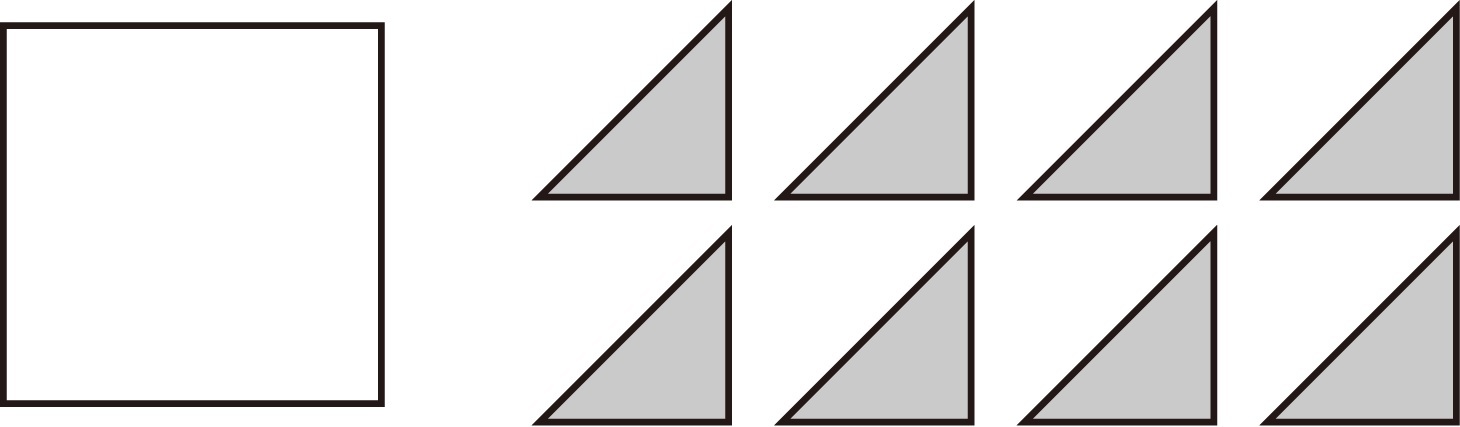
正方形を直角三角形8枚で敷き詰める場合 何通り おりぞめ染伝人ブログ

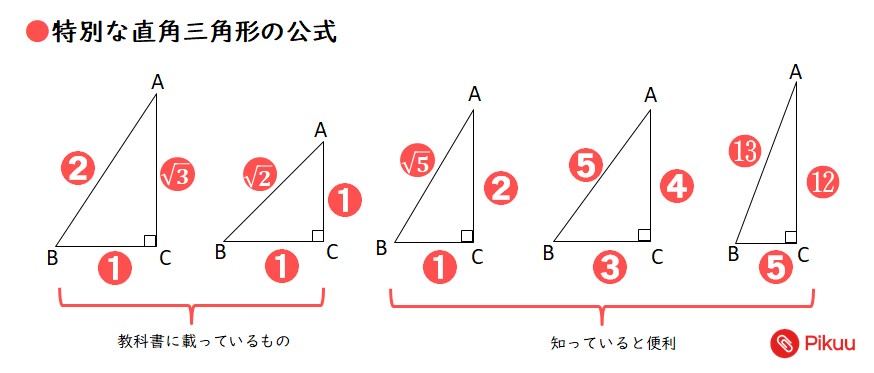
高校入試対策数学 特別な直角三角形を使った問題 Pikuu

三平方の定理 覚えておきたい基本公式を解説 数スタ

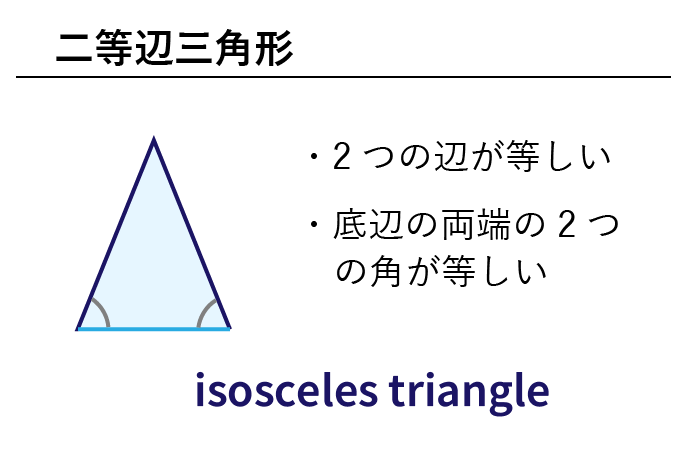
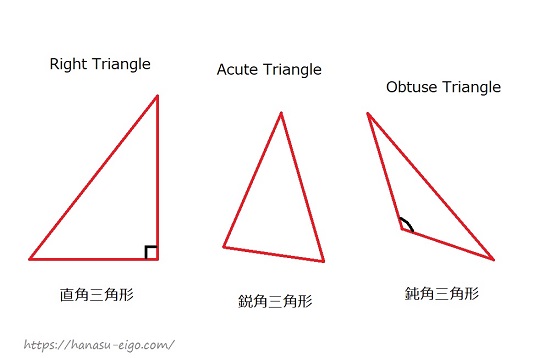
数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project

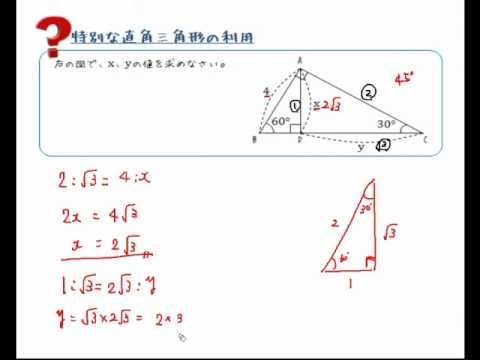
特別な直角三角形の利用 Youtube

1

B X Lihat Cara Penyelesaian Di Qanda

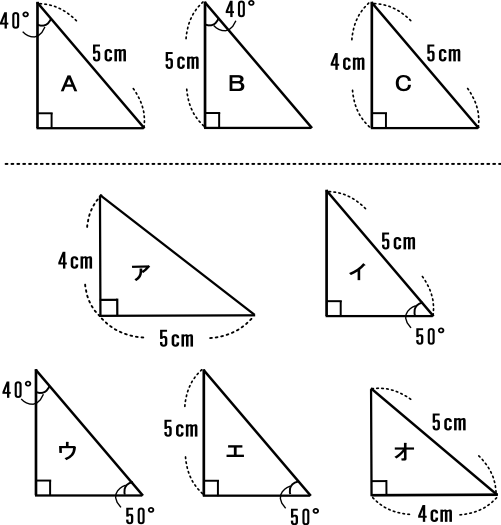
中学２年数学練習問題 直角三角形の合同条件と証明問題 図形と合同

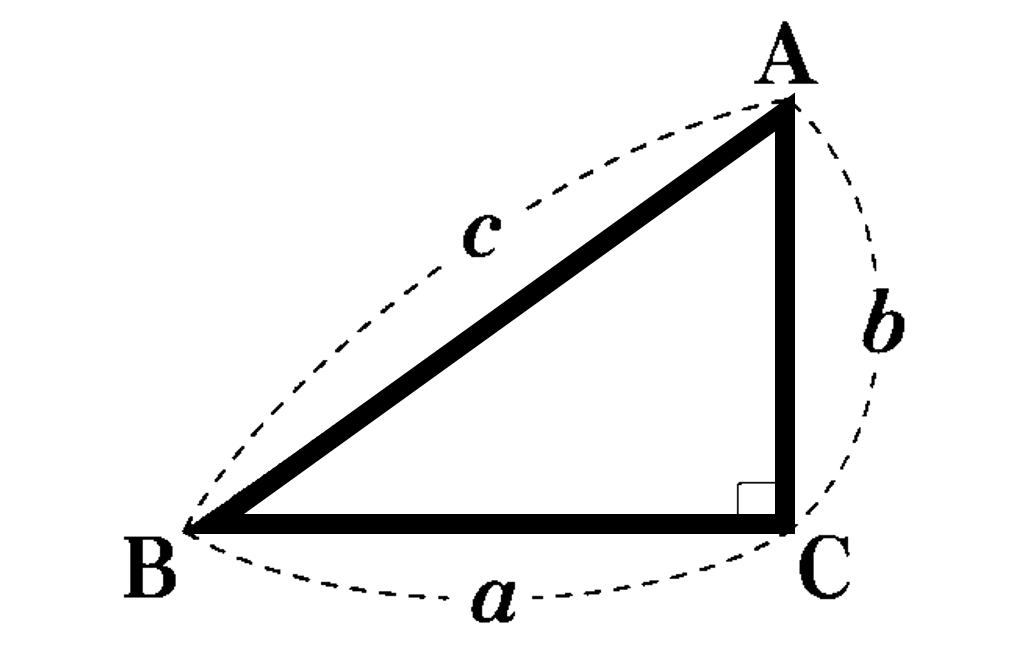
７章 三平方の定理 タカラゼミ

特別な直角三角形 Youtube

Support Education Ne Jp Ela Katsuyou Elacon T J3ma Pdf

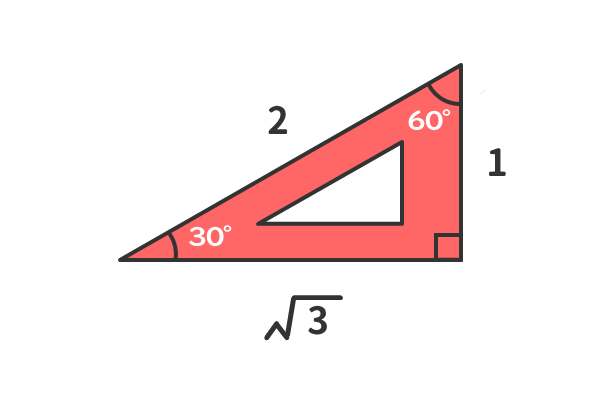
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

直角三角形の新着記事 アメーバブログ アメブロ

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Www Chuo Tky Ed Jp Ginza Jh Index Cfm 1 C Html 2105 1748 Pdf

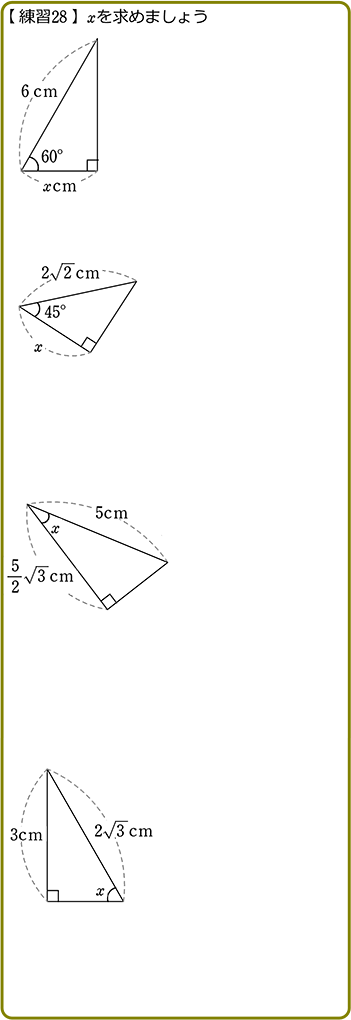
中学数学 三平方の定理

正弦定理って何か 一歩一歩ぐんぐんブログ

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

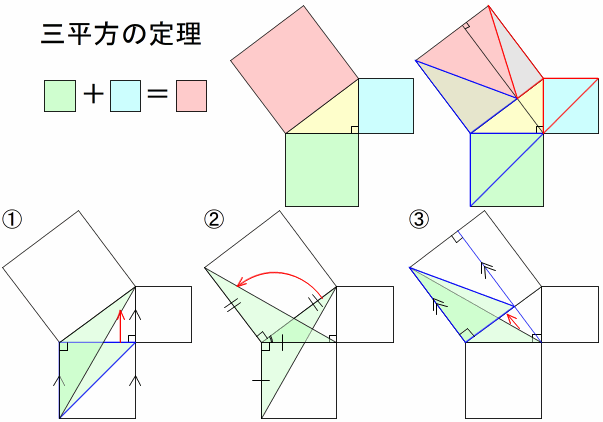
これは誤解 これが正解

三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

三平方の定理 数学入門用 Kyokuryo Math

３ ４ ５の三角形で 本当に直角ができる Note Board

三平方の定理を使って面積を求める 無料で使える中学学習プリント

三平方の定理の証明と使い方

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

高校受験入試で頻出 特別な三角形 四角形の定義とその証明

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

数学小話 ３ ４ ５の直角三角形の鋭角は何度 日比谷高校のススメ

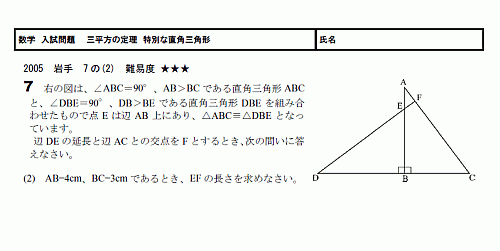
三平方の定理 スタディーx

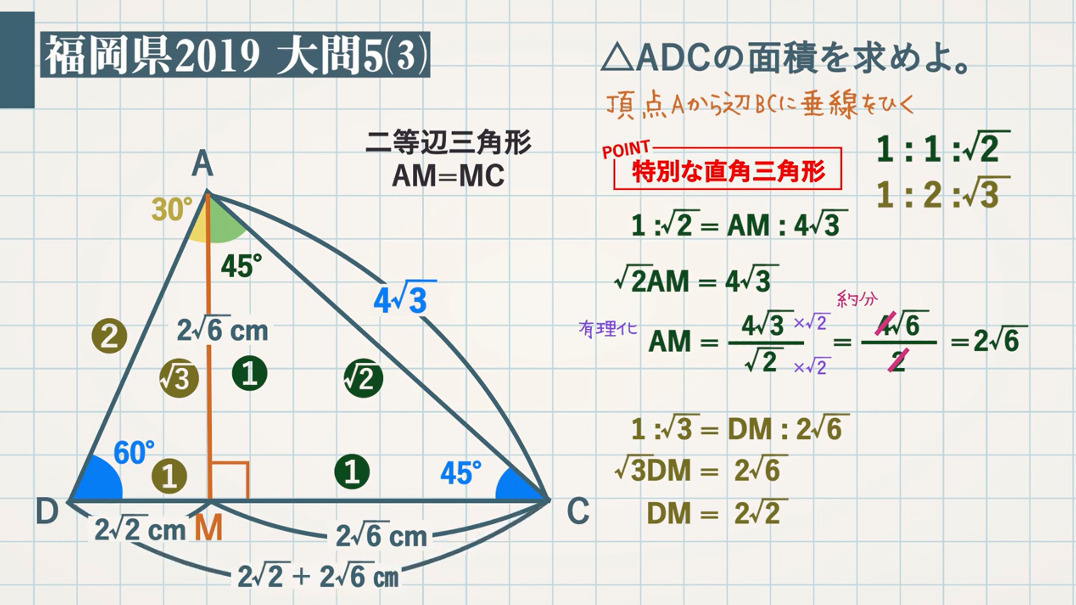
円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者

三平方の定理の利用 １ きっずゼミ子育て応援ブログ

三角形 辺 の 長 さ 比率 238n424 Proxydns Com

特別な角をもつ直角三角形 Kyokuryo Math

直角三角形の斜辺の長さを求める 3つの方法 Wikihow

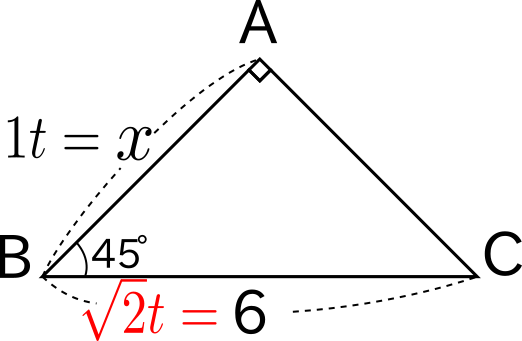
直角三角形の辺の比を文字式として利用する方法 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール

中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

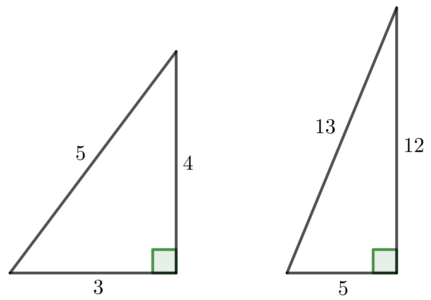
中学数学の公式一覧 図形や関数 計算 方程式 確率まで

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

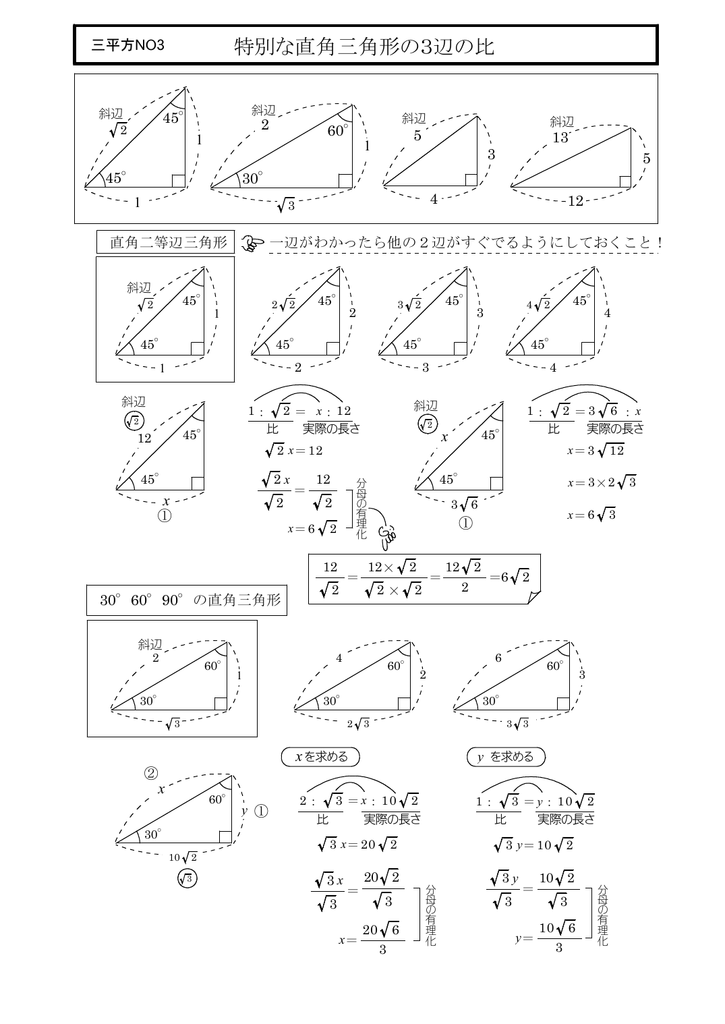
特別な直角三角形の3辺の比

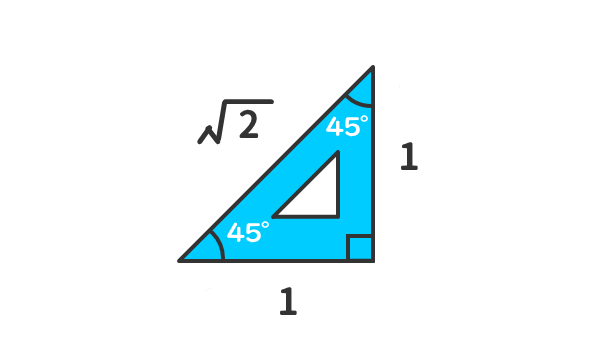
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

特別な直角三角形 問題 On Vimeo

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

1

中3数学 三平方の定理 空間図形への利用 練習問題

特別な直角三角形の３辺の比 の問題が分からないんですけど やり方を教えてください Clear

中３数学 三平方の定理 03 1 特別な直角三角形の比 解説 Youtube

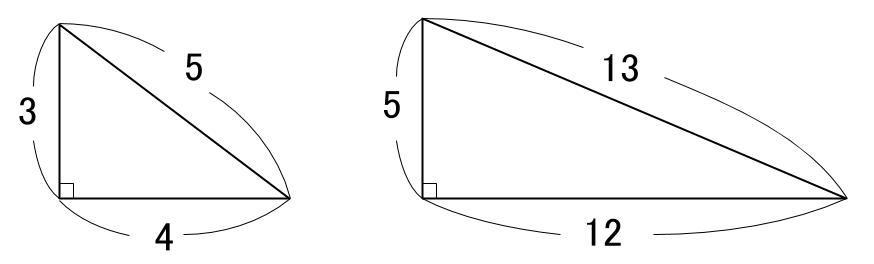
中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

直角三角形の合同条件 算数 数学が好きになりmath

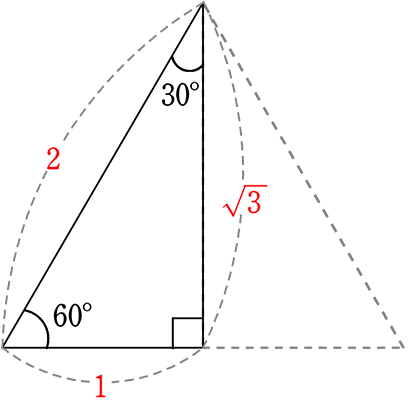
中学数学 三平方の定理

二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

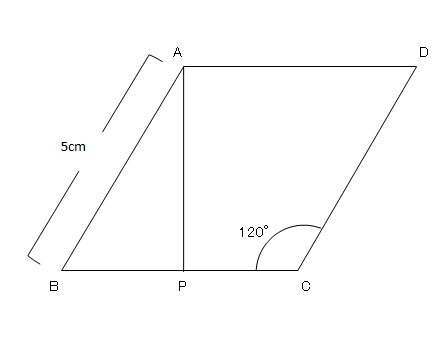
三平方の定理 特別な直角三角形 3 ネット塾

B X Lihat Cara Penyelesaian Di Qanda

Tossランド 特別な直角三角形の辺の比の復習のさせ方

Amazon Co Jp 中学 数学 3年 基礎 問題集 6 三平方の定理 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 Dvd Rom Dvd

タンジェントとは何か 中学生でも分かる三角関数の基礎

三平方の定理の利用 １ きっずゼミ子育て応援ブログ

1

三平方の定理 覚えておきたい基本公式を解説 数スタ

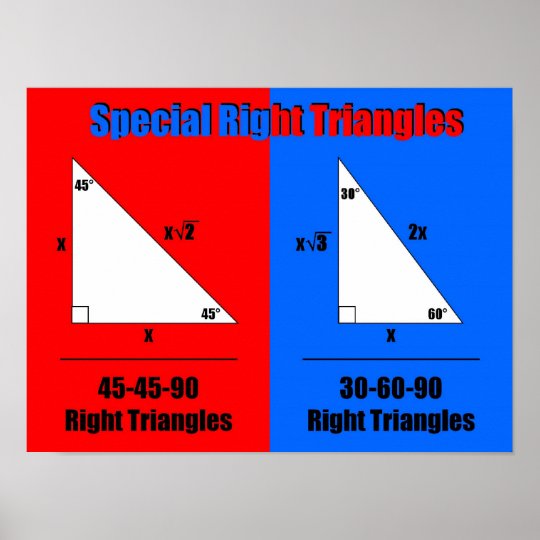
特別な直角三角形 ポスター Zazzle Co Jp

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者

Xp9ax13dult21c0wtxqar30g7ld Com Tokyo Sugaku H30 07 Q4

数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project

見本pdf 新中学問題集 発展編 塾用教材 教育開発出版株式会社 Scm H S3 Mihon

三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

数学講師向け 特別な直角三角形の辺の比はなぜ成り立つのか 塾講師ステーション情報局

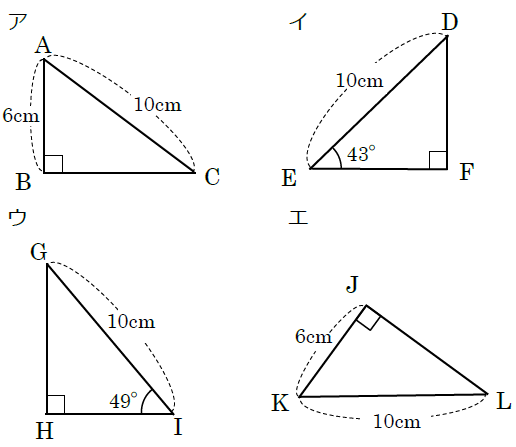
中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

中学数学 覚えておくと得する三角比 ジャムと愉快な仲間たち 0名

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

中2数学 直角三角形の合同条件 例題編 映像授業のtry It トライイット

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

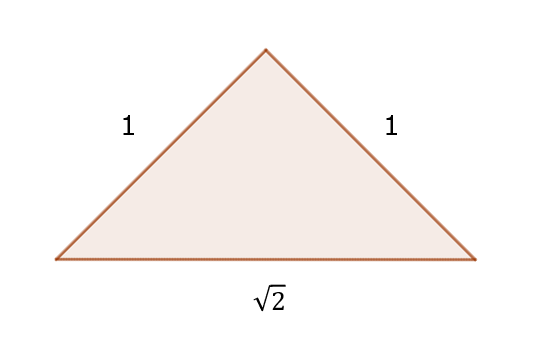
1 1 ルート2 三角形

世界に一つだけの 三角形ペア 発見 慶大院生２人証明 朝日新聞デジタル

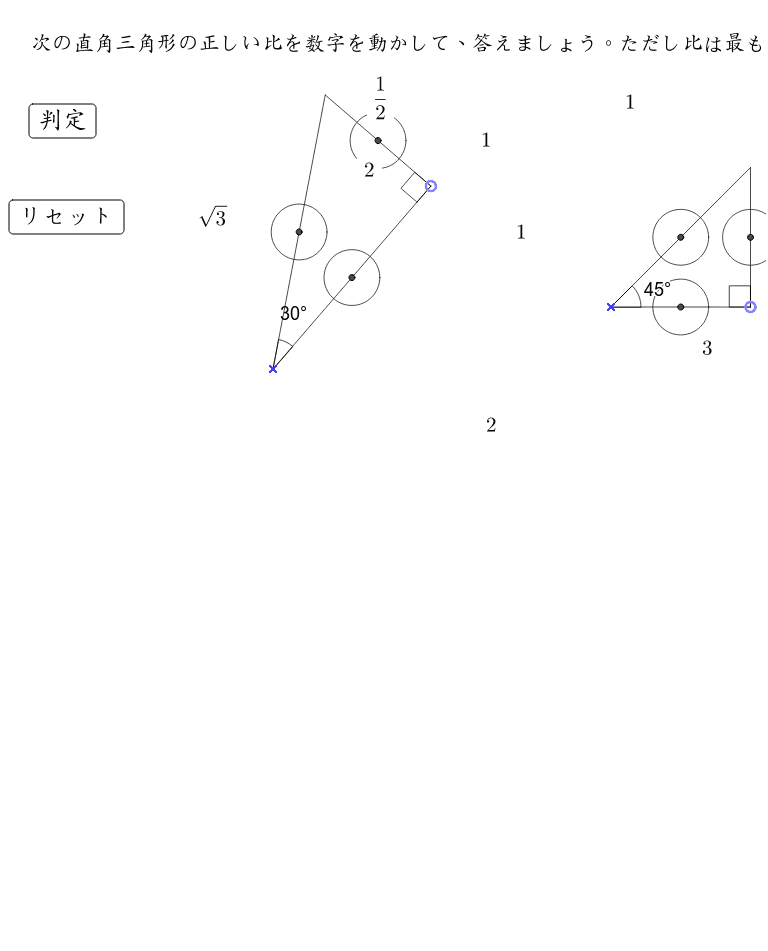
特別な三角比 Geogebra

特別な直角三角形の３辺の比 の問題が分からないんですけど やり方を教えてください Clear

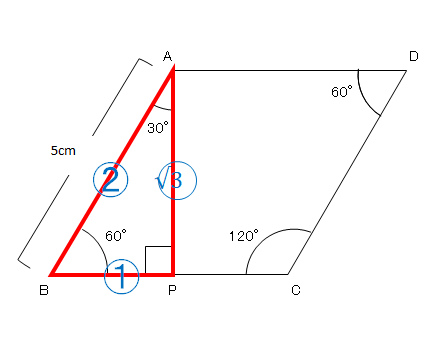
三平方の定理 特別な直角三角形 3 ネット塾

中3数学 有名角と比 映像授業のtry It トライイット

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo